Lista de exercícios de ângulos – Exercícios resolvidos
Preparamos uma lista com 5 exercícios resolvidos sobre ângulos congruentes, bissetriz de um ângulo, ângulos complementares e suplementares, e muito mais. Confira!
Muitos exercícios envolvem conhecimentos sobre ângulos, suas classificações e medidas. Nesse artigo, preparamos uma lista com 5 exercícios resolvidos sobre ângulos. Confira!
Lista de exercícios de ângulos
Exercício 1. Sabe-se que dois ângulos, AÔB e CÔD, são congruentes e que medida(AÔB) = 2x + 10° e medida(CÔD) = 130°. Qual é o valor de x ?
Exercício 2. Quando traçamos a bissetriz de um ângulo de 50° graus, obtemos dois ângulos congruentes. Quanto mede cada um desses ângulos?
Exercício 3. Encontre o valor de x e depois determine o valor, em graus, de a e de b , sabendo que:
- a = 4x + 30°
- b = x
- a + b = 180°
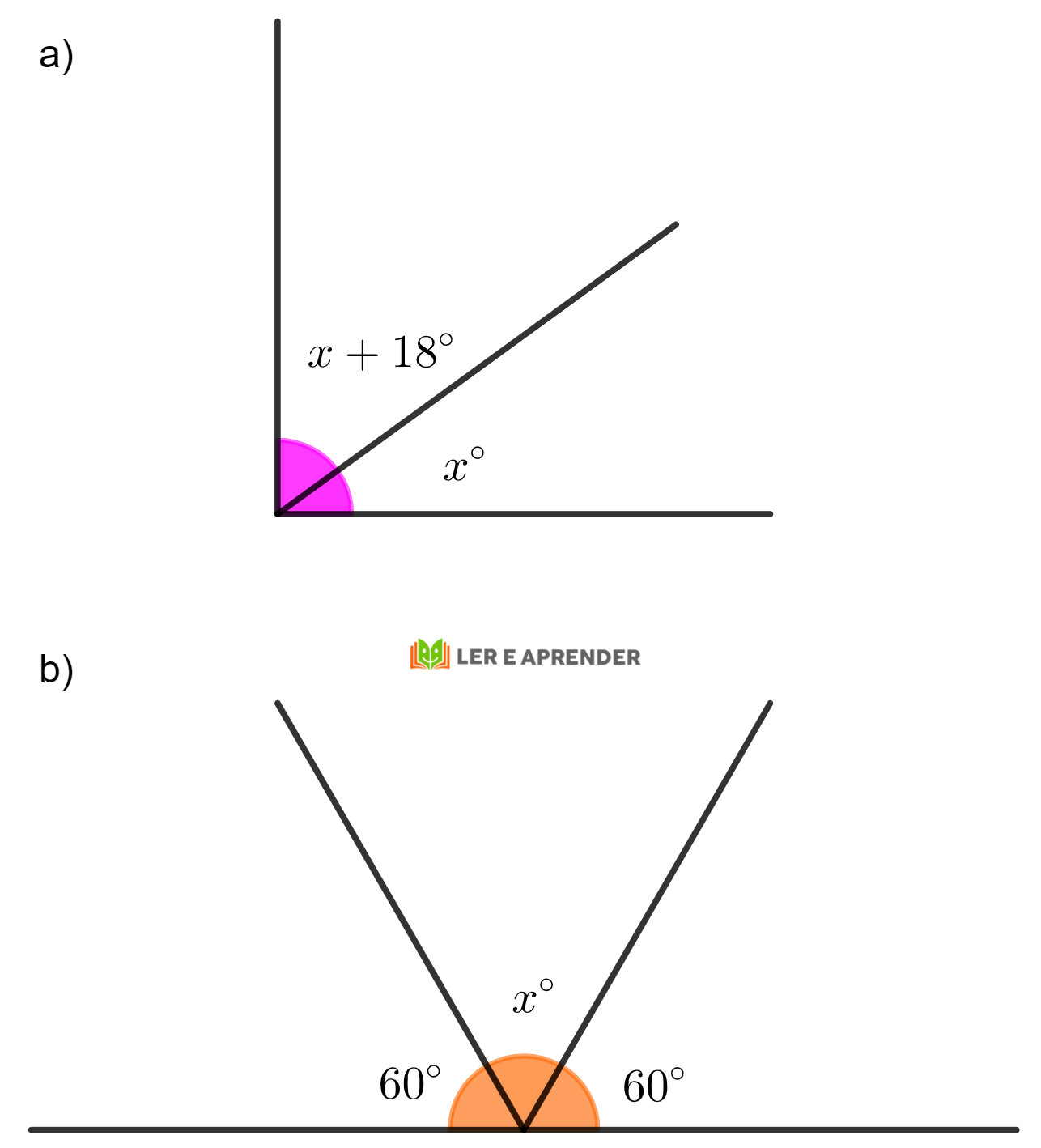
Exercício 4. Descubra o valor, em graus, da medida x em cada uma das figuras a seguir.
Exercício 5. Determine a medida do:
a) complemento do ângulo de 47º.
b) complemento do ângulo de 20º.
c) suplemento do ângulo de 135º.
d) suplemento do ângulo de 6º.
Gabarito
Resposta do exercício 1
Se dois ângulos são congruentes, então eles têm a mesma medida. Ou seja,
medida(AÔB) = medida(CÔD)
Assim, temos que:
2x + 10° = 130°
Agora, só temos que resolver essa equação, isolando a incógnita x.
2x + 10° = 130°
2x = 130° – 10°
2x = 120°
x = 120° / 2
x = 60°
Então, o valor de x é 60°.
Resposta do exercício 2
A bissetriz é uma semirreta que divide um ângulo em dois ângulos congruentes, ou seja, de mesma medida.
Assim, se o ângulo mede 50°, a bissetriz divide esse ângulo em dois ângulos de 25°, pois 50/2 = 25.
Resposta do exercício 3
Para resolver esse exercício, temos que substituir os valores de a e de b na expressão a + b = 180° .
Temos a = 4x + 30° e b = x. Vamos substituir e, depois, isolar a incógnita x:
a + b = 180°
4x + 30° + x = 180°
4x + x = 180° – 30°
5x = 150°
x = 150° / 5
x = 30°
Então, o valor de x é 30°. Agora, vamos determinar o valor de a:
a= 4x + 30°
a = 4. 30° + 30°
a = 120° + 30°
a = 150°
E o valor de b:
b = x
b = 30°
Resposta do exercício 4
a) Os dois ângulo juntos formam um ângulo de 90º, ou seja, se somarmos as medidas desses ângulos, x + 18º e xº, o resultado deve ser igual a 90º.
Assim, temos que resolver a seguinte equação:
x + 18º + x = 90°
Vamos isolar x:
x + 18º + x = 90°
x + x = 90º – 18º
2x = 72º
x = 72º / 2
x = 36º
Então, o valor de x é igual a 36°.
b) Os três ângulos juntos formam um ângulo de 180º, ou seja, se somarmos as medidas desses ângulos, 60°, x° e 60°, o resultado deve ser igual a 180º.
Assim, temos que resolver a seguinte equação:
60° + x + 60° = 180°
Vamos isolar x:
60° + x + 60° = 180°
x = 180° – 60° – 60°
x= 180° – 120°
x = 60°
Então, o valor de x é igual a 60°.
Resposta do exercício 5
a) Para saber qual o complemento de um ângulo de 47°, basta calcular:
90° – 47° = 43°
O complemento é o ângulo de 43°.
b) Para saber qual o complemento de um ângulo de 20°, basta calcular:
90° – 20° = 70°
O complemento é o ângulo de 70°.
c) Para saber qual o suplemento de um ângulo de 135°, basta calcular:
180° – 135° = 45°
O complemento é o ângulo de 45°.
d) Para saber qual o suplemento de um ângulo de 6°, basta calcular:
180° – 6° = 174°
O suplemento é o ângulo de 174°.
Para baixar essa lista em pdf, clique aqui!
Você também pode se interessar: