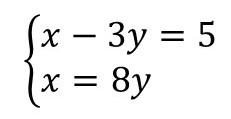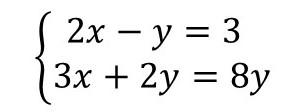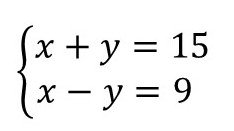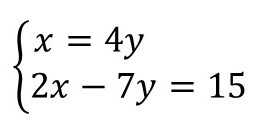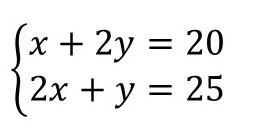Exercícios de sistemas de equação do 1° grau
Veja uma lista com cinco exercícios resolvidos sobre sistemas de equações do 1° grau e aprenda a resolver sistemas passo a passo.
Um sistema de equações do 1° grau é formado por um conjunto de equações do 1° grau que devem ser resolvidas de forma simultânea. Assim, os valores das incógnitas devem ser encontrados de forma que satisfaçam todas as equações do sistema.
Veja como fazer isso através de uma lista de exercícios resolvidos que preparamos sobre sistemas de equações do 1° grau.
Lista de exercícios de sistemas de equação do 1° grau
Exercício 1. Monte um sistema de equações que represente a seguinte situação:
- Um sanduíche e dois refrigerantes custam 20 reais;
- Dois sanduíches e um refrigerante custam 25 reais.
Exercício 2. Verifique se o par ordenado (8, 1) é solução do sistema de equações abaixo:
Exercício 3. Verifique se o par ordenado (2, 3) é solução do sistema abaixo:
Exercício 4. Encontre a solução do seguinte sistema de equações:
Exercício 5. Encontre a solução do seguinte sistema de equações:
Gabarito
Respostas do exercício 1
Considere:
x : preço do sanduíche
y : preço do refrigerante
Então:
Um sanduíche e dois refrigerantes custam 20 reais → x + 2y = 20
Dois sanduíches e um refrigerante custam 25 reais → 2x + y = 25
Assim, o sistema de equações é:
Respostas do exercício 2
Para verificar se um par ordenado é solução de um sistema de equações, basta substituir os valores de x e y nas equações. Se as igualdades forem verdadeiras, então, é solução.
Temos o par ordenado (8, 1), então x = 8 e y = 1. Vamos substituir na primeira equação:
x – 3y = 5
8 – 3. 1 = 5
8 – 3 = 5
5 = 5
Substituindo na segunda equação:
x = 8y
8 = 8.1
8 = 8
Chegamos a igualdades verdadeiras, então, o par ordenado é solução do sistema.
Respostas do exercício 3
Temos o par ordenado (2, 3), então x = 2 e y = 3. Vamos substituir na primeira equação:
2x – y = 3
2.2 – 3 = 3
4 – 3 = 3
1 = 3 → 1 não é igual a 3! Chegamos a uma igualdade que não é verdadeira.
Nem precisamos substituir os valores na segunda equação, pois para ser solução, deve satisfazer as duas equações. Se a primeira não foi satisfeita, já podemos concluir que o par ordenado não é solução do sistema dado.
Respostas do exercício 4
Vamos resolver pelo método da substituição.
Vamos isolar a incógnita x na primeira equação:
x + y = 15
x = 15 – y
Substituímos x por 15 – y na segunda equação:
x – y = 9
15 – y – y = 9
15 – 2y = 9
-2y = 9 – 15
-2y = -6
y = 6/2
y = 3
Substituímos o valor de y por 3 e encontramos o valor de x:
x = 15 – y
x = 15 – 3
x = 12
Logo, a solução do sistema é o par ordenado (12, 3).
Respostas do exercício 5
Vamos resolver pelo método da substituição.
Observe que a incógnita x já está isolada na primeira equação, temos x = 4y.
Vamos substituir o valor de x por 4y na segunda equação:
2x – 7y = 15
2. (4y) – 7y = 15
8y – 7y = 15
1y = 15
y = 15/1
y = 15
Substituímos o valor de y por 15 e encontramos o valor de x:
x = 4y
x = 4 . 15
x = 60
Portanto, a solução do sistema é o par ordenado (60, 15).
Para baixar essa lista em PDF, clique aqui!
Você também pode se interessar: