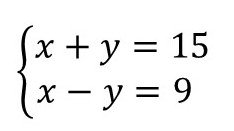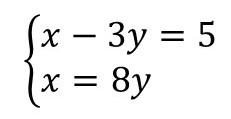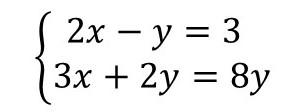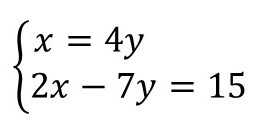Exercícios de sistemas de equações – Método da adição
Preparamos uma lista de exercícios resolvidos sobre sistemas de equações do 1° grau utilizando o método da adição. Confira e aprenda a usar esse método!
Em um sistema de equações do 1° grau devemos encontrar os valores das incógnitas que sejam solução de todas as equações do sistema ao mesmo tempo. Para isso, existem alguns métodos diferentes, como o método da adição.
O método da adição consiste em somar as equações para “sumir” com uma das incógnitas. Mas muitas vezes, antes de somar as equações, precisamos multiplicar uma (ou as duas) equação por um número.
Veja como fazer isso a partir de uma lista de exercícios resolvidos que preparamos sobre sistemas de equações do 1° grau pelo método da adição.
Lista de exercícios de sistemas de equação do 1° grau – método da adição
Exercício 1. Encontre a solução do seguinte sistema de equações pelo método da adição.
Exercício 2. Calcule a solução do sistema de equações abaixo pelo método da adição.
Exercício 3. A solução do sistema abaixo é o par ordenado (2.1). Mostre que isso é verdade resolvendo o sistema pelo método da adição.
Exercício 4. Determine a solução do sistema a seguir pelo método da adição.
Gabarito
Respostas do exercício 1
Observe que temos termos opostos nas duas equações: + y na equação 1 e -y na equação 2. Então, se somarmos essas duas equações, termo a termo, a incógnita y irá “sumir”, pois + y – y = 0.
Temos:
x + y = 15 → equação 1
x – y = 9 → equação 2
Somando essas duas equações: → 2x = 24.
Agora, resolvendo essa equação, podemos encontrar o valor de x.
2x = 24
x = 24/2
x = 12
Substituindo o valor de x por 12 na equação 1, temos que:
x + y = 15
12 + y = 15
y = 15 – 12
y = 3
Assim, a solução do sistema é o par ordenado (12, 3).
Respostas do exercício 2
Primeiro, vamos organizar a segunda equação, deixando todos os termos com incógnitas do lado esquerdo.
x = 8y
x – 8y = 0
Agora, vamos multiplicar essa equação por (-1).
x – 8y = 0 (-1)
– x + 8y = 0
Observe que fazendo isso obtemos termos opostos nas duas equações: x e -x. Portanto, somando as duas equações, termo a termo, conseguimos “sumir” com a incógnita x.
x – 3y = 5 → equação 1
– x + 8y = 0 → equação 2
Somando as duas → +5y = 5.
Resolvendo para encontrar y:
+5y = 5
y = 5/5
y = 1
Substituindo o valor de y por 1 na equação 1:
x – 3y = 5
x – 3(1) = 5
x – 3 = 5
x = 5 + 3
x = 8
Logo, a solução do sistema é o par ordenado (8,1).
Respostas do exercício 3
Primeiro, vamos organizar a segunda equação, deixando todos os termos com incógnitas do lado esquerdo.
3x + 2y = 8y
3x + 2y – 8y = 0
3x – 6y = 0
Ficamos com as seguintes equações:
2x – y = 3 → equação 1
3x – 6y = 0 → equação 2
Agora, para obter termos opostos vamos multiplicar a equação 1 pelo número (- 6).
2x – y = 3 (- 6)
-12x + 6y = – 18
Com isso, temos:
-12x + 6y = – 18 → equação 1
3x – 6y = 0 → equação 2
Os termos +6y e -6y são termos opostos. Isso significa que se somarmos essas duas equações, a incógnita y irá “sumir” e poderemos encontrar o valor de x.
Somando essas duas equações: → -9x = -18
Resolvendo para encontrar o valor de x:
-9x = -18
x = 18/9
x = 2
Substituindo o valor de x por 2 na equação 1, temos que:
-12x + 6y = – 18
-12 . 2 + 6y = -18
-24 + 6y = -18
6y = -18 + 24
6y = 6
y = 6/6
y = 1
Então, a solução do sistema é o par ordenado (2, 1).
Respostas do exercício 4
Organizando a primeira equação:
x = 4y
x – 4y = 0
Multiplicando essa equação por (-2):
x – 4y = 0 (-2)
-2 x + 8y = 0
Assim, obtemos os termos opostos – 2x e + 2x.
-2x + 8y = 0 → equação 1
2x – 7y = 15 → equação 2
Somando essas duas equações → y = 15
Substituindo o valor de y por 15 na equação 1, temos que:
-2x + 8y = 0
– 2x + 8 . 15 = 0
– 2x + 8 . 15 = 0
-2x +120 = 0
-2x = -120
x = 120/2
x = 60
Portanto, a solução do sistema é o par ordenado (60, 15).
Para baixar essa lista em PDF, clique aqui!
Você também pode se interessar: