Números racionais
Saiba quais são os números racionais e veja exemplos. Aprenda também, quais são os subconjuntos formados por esse tipo de número.
Os números racionais são todas as frações e todos os números que podem ser escritos como frações.
Exemplos de frações:
1/3 → Lê-se: um terço
2/5 → Lê-se: dois quintos
7/8 → Lê-se: sete oitavos
Exemplos de números que podem ser escritos como frações:
1 = 10/10
4 = 8/2
-15 = – 60/4
0,1 = 1/10
0,34 = 34/100
Assim, todos esses números são números racionais.
Conjunto dos números racionais
O conjunto formado por todos os números racionais é representado pela letra Q. O uso da letra Q vem da palavra quociente, já que toda fração é um quociente (divisão).
Lembre-se que:
1/2 = 1 : 2 10/ 4 = 10 : 4 3/20 = 3 : 20
Como qualquer número inteiro, seja positivo ou negativo, pode ser escrito como uma fração, então qualquer número inteiro é também um número racional.
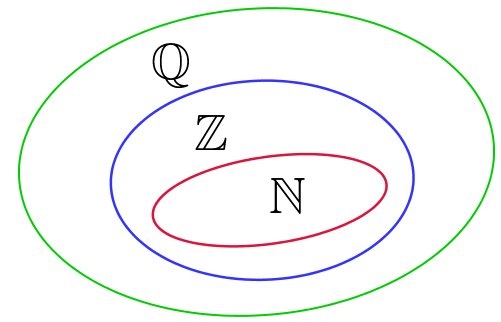
Assim, o conjunto dos números inteiros (Z), o qual contém os naturais (N), está dentro do conjunto dos racionais. Veja a representação:
Além disso, o conjunto Q possui alguns subconjuntos, que são conjuntos menores dele mesmo.
Q* → Conjunto dos números racionais sem o zero.
Q+ → Conjunto dos números racionais sem os números negativos.
Q*+ → Conjunto dos números racionais sem os números negativos e sem o zero.
Q _ → Conjunto dos números racionais sem os números positivos.
Q*_ → Conjunto dos números racionais sem os números positivos e sem o zero.
Exemplos de números racionais
Que são números Inteiros:
8/1=8
3/1=3
-4/1=4
Que são números decimais finitos:
4/10= 0,4
8/100= 0.08
3587/1000=3,587
Que são número decimais infinitos, mas periódicos:
5/6= 0.83333333333…
592/877=0.67502850627
32/3= 10.6666666667
Dessa maneira, após apresentar o que são os números racionais, é possível concluir que as frações e os números decimais (finitos ou infinitos periódicos) possuem esta característica em comum: fazem parte do conjunto Q.
Você também pode se interessar: