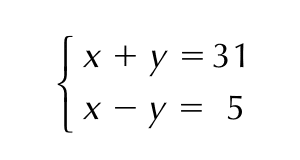Equação do 1° grau
Saiba o que são as equações do 1° grau e aprenda como resolvê-las. Além disso, veja o que são os sistemas de equações.
Lembrando que o expoente 1, normalmente, é omitido. Assim x¹ ou y¹ aparecem nas equações escritos como x ou y, apenas.
Exemplos de equações do 1° grau:
a) x + 1 = 0
b) 2x + x = 4
c) 0,5 x – 2 = 1,4
d) 4x + 5y -1 = 0
Uma equação do 1° grau pode ter mais do que uma incógnita, veja que no item (d) temos x e y, duas incógnitas. Isso não faz com que a equação não seja do 1° grau. No entanto, se tivéssemos x² ou y³, por exemplo, a equação não seria mais do 1° grau.
Agora que já sabemos o que são as equações do primeiro, vamos ver como resolvê-las.
Como resolver uma equação do 1° grau
Resolver uma equação do 1° grau significa encontrar o valor da incógnita. Vamos ver como fazer isso através de exemplos.
Exemplos:
a) x – 4 = 1
Vamos isolar a incógnita x, deixando apenas ela do lado esquerdo. Para isso, vamos passar o número – 4 para o outro lado da igualdade.
Um número com sinal de menos (-) passa para o outro lado sempre com sinal de mais (+).
x – 4 = 1
x = 1 + 4
Agora, a incógnita já está isolada. O próximo passo é resolver a operação do lado direito da igualdade.
Como 1 + 4 = 5, temos que:
x = 5
b) 2x + x + 1 = 7
Nessa equação, temos mais de um termo com a incógnita x, todos eles devem ficar isolados do lado esquerdo. Para isso, vamos passar o número +1 para o outro lado da igualdade.
Um número com sinal de mais (+) passa para o outro lado com o sinal de menos (-).
2x + x + 1 = 7
2x + x = 7 -1
Agora, a incógnita já está isolada. O próximo passo é resolver a operação dos dois lados da igualdade.
Como 2x + x = 3x e 7 -1 = 6, temos que:
3x = 6
Observe que a incógnita x está multiplicada pelo número 3. Devemos passar o número 3 para o outro lado da equação.
Um número que está multiplicando (.), passa para o outro lado dividindo (÷).
3x = 6
x = 6 ÷ 3
Agora, temos que resolver a operação do lado direito da igualdade.
Como 6 ÷ 3 = 2, temos que:
x = 2
c) x – 4 = – x + 8
Vamos resolver essa equação de uma forma direta e prática. Cada uma das linhas indica que foi feita uma operação ou alguma mudança na equação.
x – 4 = – x + 8
x + x = +8 + 4
2x = 12
x = 12 ÷ 2
x = 6
Sistema de equações do 1° grau
Um sistema de equações do 1° grau é formado por um conjunto de equações do 1° grau, que devem ser resolvidas ao mesmo tempo. Supondo que temos duas equações com incógnita x, então devemos resolver as duas equações para encontrar o valor de x que é solução das duas equações.
Exemplo: As equações x + y = 31 e x – y = 5 são equações do 1° grau com duas incógnitas. Um sistema formado por essas duas equações é:
Existem alguns métodos para resolver um sistema de equações, como o método da adição. Contudo, independente do método utilizado, a solução é sempre a mesma. Nesse sistema, a solução é o par ordenado (x, y) = (18, 13).
Veja que: 18 + 13 = 31 e que 18 – 13 = 5, ou seja, essa é realmente uma solução para as duas equações.
Você também pode se interessar: