Exercícios de transformações de medidas de ângulos
Aprenda a fazer transformações entre graus, minutos e segundos com uma lista de exercícios sobre transformações de medidas de ângulos. Todos os exercícios resolvidos!
Existem ângulos que não possuem como medida um número inteiro, por exemplo 17,5°. Assim, para facilitar cálculos e operações envolvendo medidas como essa, são utilizados os submúltiplos do grau: os minutos e os segundos.
As relações envolvendo o grau e seus submúltiplos são:
- 1° = 60′ → 1 grau é igual a 60 minutos.
- 1′ = 60″ → 1 minuto é igual a 60 segundos.
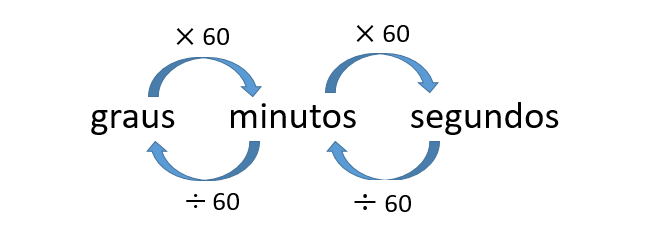
Podemos fazer transformações entre medidas de ângulos, da seguinte forma:
A seguir, veja uma lista com cinco exercícios resolvidos sobre transformações de medidas de ângulos.
Lista de exercícios de transformações de medidas de ângulos
Exercício 1. Transforme 10’20” em segundos.
Exercício 2. Transforme 20° 40′ em minutos.
Exercício 3. Transforme 90′ em graus.
Exercício 4. Escreva 37°128′ como uma medida em graus e minutos, mas na forma simplificada.
Exercício 5. Escreva cada uma das medidas em graus, minutos e segundos, fazendo as simplificações necessárias.
Gabarito
Respostas do exercício 1
Queremos transformar 10’20” em segundos. Observe que uma parte dessa medida de ângulo já está em segundos, temos 20″. Só precisamos transformar a parte que está em minutos.
Assim, o que temos que fazer é transformar 10′ em segundos e depois somar com os segundos que já temos.
Para transformar minutos em segundos, basta multiplicar por 60:
10 x 60 = 600
Logo, 10′ = 600″.
Então, 10’20” = 600″ + 20″ = 620″.
Respostas do exercício 2
Queremos transformar 20° 40′ em minutos. Novamente, uma parte da medida do ângulo já está em minutos. Só precisamos transformar a parte que está em graus.
Assim, o que temos que fazer é transformar 20° em minutos e depois somar com os minutos que já temos.
Para transformar graus em minutos, basta multiplicar por 60:
20 x 60 = 1200
Logo, 20° = 1200′.
Então, 20° 40′ = 1200′ + 40′ = 1240′.
Respostas do exercício 3
Queremos transformar 90′ em graus.
Para transformar segundos em minutos, basta dividir por 60:
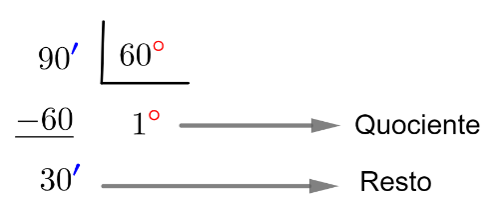
90′ ÷ 60 °
Realizamos a conta de dividir até encontrar o quociente e o resto, ou seja, não adicionamos vírgula na conta. Desse modo, o quociente obtido foi 1 e o resto 30, o que significa que:
90′ = 1°30′.
Respostas do exercício 4
Queremos escrever 37°128′ como uma medida em graus e minutos, mas de forma simplificada. Isso significa fazer uma transformação necessária para que os minutos sejam menores que 60.
Vamos utilizar a relação entre graus e minutos:
1° = 60′
Assim, 128′ = 60′ + 60′ +8′ = 1° + 1° + 8′ = 2° + 8′.
Logo, 37°128′ = 37° + 2° + 8′ = 39° 8′.
Respostas do exercício 5
a) 17°70’85”
Queremos simplificar, ou seja, escrever uma medida que tenha menos do que 60 segundos e menos do que 60 minutos.
Vamos começar pelos segundos. A relação entre minutos e segundos é:
1′ = 60″
Então, 85″ = 60″ + 25″ = 1′ + 25″
Logo, 17°70’85” = 17° + 70′ + 1′ + 25″ = 17°71’25”
Agora, vamos para os minutos. A relação entre graus e minutos é:
1° = 60′
Então, 71′ = 60′ + 11′ = 1°11′.
Logo, 17°71’25” = 17° + 1° + 11′ + 25″ = 18°11’25”.
b) 66°124’190″
De modo similar, utilizando a relação entre minutos e segundos, temos que 190″ = 3′ + 10″
Logo, 66°124’190″ = 66° + 124′ + 3′ + 10″ = 66° 127’10”
Agora, utilizando a relação entre graus e minutos, temos que 127′ = 2° + 7′.
Assim, 66° 127’10” = 66° + 2° + 7′ +10″ = 68° 7’10”.
Para baixar essa lista em PDF, clique aqui!
Você também pode se interessar: