Multiplicação de frações

Entenda o que é e veja como fazer a multiplicação de uma fração por um número inteiro e a multiplicação entre duas frações, de um jeito bem fácil.

As frações são uma forma de escrever números que representam quantidades não inteiras e em muitas situações, precisamos fazer a multiplicação de frações.

O que é a multiplicação de fração? A multiplicação de fração nada mais é do que a multiplicação de uma fração por um número inteiro ou então por uma outra fração.

Quer aprender como fazer multiplicação de fração? Está no post certo!

Multiplicação de fração por número inteiro

Para entender como funciona a multiplicação de fração por um número inteiro, imagine que você tem 6 maçãs e parte todas ao meio. Assim, você fica com 12 metades, certo?

Cada metade de maçã pode ser representada pela fração $\frac{1}{2}$ . Qual a quantidade de maçã que você teria se juntasse seis dessas metades?

Para saber a reposta, basta somar $\frac{1}{2}$ seis vezes que é o mesmo que multiplicar essa fração pelo número 6.

$\frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} = 6 \times \frac{1}{2} = \frac{6}{2} = 3$

Ou seja, a multiplicação de uma fração por um número inteiro pode ser obtida a partir de uma soma de fração. Contudo, existe um jeito mais prático de realizar a multiplicação de fração:

Para multiplicar um número inteiro por uma fração, basta multiplicar o número pelo numerador da fração e conservar o denominador.

Exemplos:

$\mathbf{4 \times \frac{2}{15} = \frac{4\times 2}{15} = \frac{8}{15}}$

$\mathbf{5 \times \frac{3}{20} = \frac{5 \times 3}{20} = \frac{15}{20} = \frac{3}{4}}$

Multiplicação de duas frações

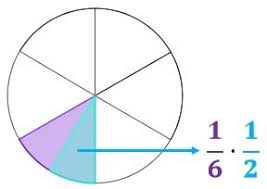
Vamos entender o que é a multiplicação de duas frações, considerando o exemplo da figura abaixo. Temos um disco dividido em seis partes iguais e gostaríamos de saber quanto é metade de uma dessas partes, ou seja, quanto é $\frac{1}{2}$ de $\frac{1}{6}$ .

Observando a figura, podemos deduzir que a parte azul que representa $\frac{1}{2}$ de $\frac{1}{6}$ . corresponde a $\frac{1}{12}$ , isto é, seria o mesmo que dividir o disco em 12 partes e considerar apenas uma delas.

O resultado que encontramos é o resultado da multiplicação entre essas duas frações. Então, determinar quanto dá $\frac{1}{2}$ de $\frac{1}{6}$ é o mesmo que calcular $\frac{1}{2} \times \frac{1}{6}$ .