Lista de exercícios sobre teorema de Pitágoras

Confira uma lista de exercícios sobre teorema de Pitágoras, com todas as questões resolvidas!

O teorema de Pitágoras é um importante teorema da matemática que estabelece uma relação entre as medidas dos lados de um triângulo retângulo.

De acordo com o teorema, a hipotenusa ao quadrado é igual a soma dos quadrados dos catetos:

$\mathrm{a^2 = b^2 + c^2}$

Em que:
a: hipotenusa;
b e c: catetos.

Para aprender mais, confira uma lista de exercícios sobre teorema de Pitágoras, todas as questões com resolução!

Lista de exercícios sobre teorema de Pitágoras

Exercício 1. Calcule a hipotenusa de um triângulo retângulo com catetos iguais a 8 m e 15 m.

Exercício 2. Calcule a medida do lado maior de um triângulo retângulo com lados conhecidos medindo 3 cm e 4 cm.

Exercício 3. Calcule a medida do terceiro lado de um triângulo retângulo com lado maior medindo 13 cm e um outro lado medindo 5 cm.

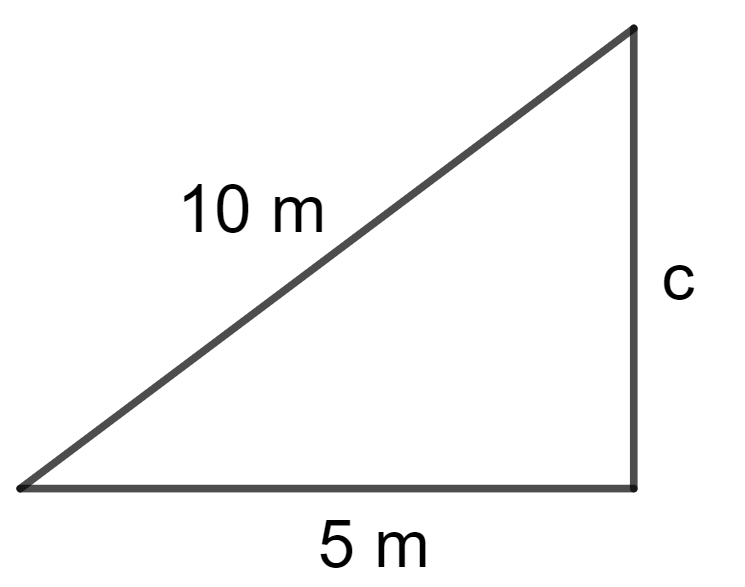
Exercício 4. Uma escada de 10 metros de comprimento está apoiada em uma parede. Sabendo que a base da escada está a 5 metros de distância da parede, determine a altura que a escada alcança na parede.

Exercício 5. Calcule a altura de um triângulo equilátero de lado igual a 6 cm.

Gabarito

Respostas do exercício 1

Vamos aplicar o teorema de Pitágoras:

$\mathrm{a^2 =8^2 + 15^2}$

$\mathrm{a^2 =64 + 225}$

$\mathrm{a^2 =289}$

$\mathrm{a =\sqrt{289}}$

$\mathrm{a =17}$

Desse modo, a hipotenusa do triângulo é igual a 17 m.

Respostas do exercício 2

O lado maior de um triângulo retângulo é sempre a hipotenusa. Assim, vamos aplicar o teorema de Pitágoras, considerando b = 3 e c = 4.

$\mathrm{a^2 = b^2 + c^2}$

$\mathrm{a^2 = 3^2 + 4^2}$

$\mathrm{a^2 = 25}$

$\mathrm{a = 5}$

Portanto, o lado maior do triângulo mede 5 cm.

Respostas do exercício 3

A hipotenusa mede 13 cm e um dos catetos mede 5 cm. Vamos aplicar o teorema de Pitágoras para determinar o outro cateto.

$\mathrm{13^2 = 5^2 + c^2}$

$\mathrm{13^2 -5^2 = c^2}$

$\mathrm{144 = c^2}$

$\mathrm{ c^2= 144}$

$\mathrm{ c= 12}$

Portanto, o terceiro lado do triângulo mede 12 cm.

Respostas do exercício 4

A medida da altura que desejamos encontrar corresponde ao lado c do triângulo retângulo abaixo.

Vamos aplicar o teorema de Pitágoras.

$\mathrm{10^2 = 5^2 + c^2}$

$\mathrm{10^2 - 5^2= c^2}$

$\mathrm{75= c^2}$

$\mathrm{c^2= 75}$

$\mathrm{c= 8,66}$

Então, a altura que a escada alcança na parede é igual a 8,66 metros.

Respostas do exercício 5

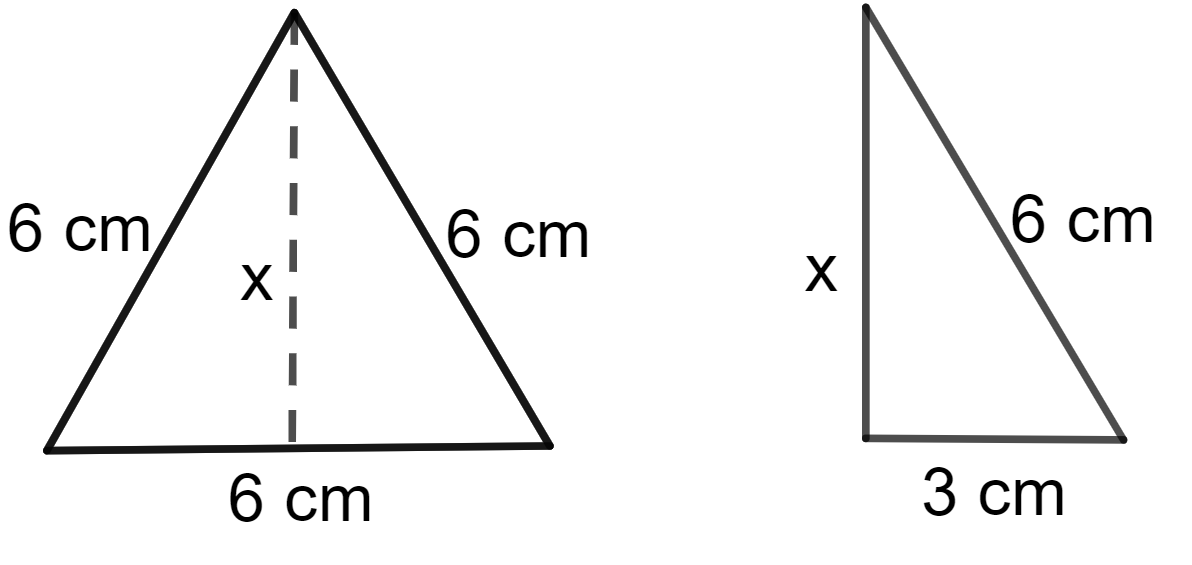
A altura x de um triângulo equilátero é um segmento que divide o triângulo em dois triângulos retângulos, conforme a figura abaixo.

Para determinar x, podemos aplicar o teorema de Pitágoras considerando hipotenusa igual a 6 cm e um dos catetos igual a 3 cm.

$\mathrm{6^2 = 3^2 + x^2}$

$\mathrm{6^2 - 3^2= x^2}$

$\mathrm{27= x^2}$

$\mathrm{x^2 = 27}$

$\mathrm{x = 5,19}$

Portanto, a altura do triângulo é igual a 5,19 cm.

Para baixar essa lista de exercícios em PDF, clique aqui!

Você também pode se interessar:

Continue lendo

Exercícios resolvidos Teorema Pitágoras