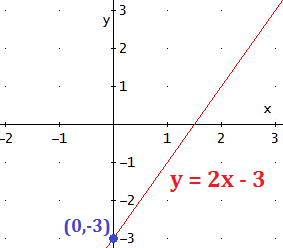Coeficiente linear
Saiba o que é o coeficiente linear na equação de uma reta e em uma função do 1° grau. Veja exemplos e tire suas dúvidas!
O coeficiente linear é um número real, podendo ser um valor positivo, negativo ou até igual a zero.
Exemplos:
y = 2x + 1 → b = 1 → coeficiente linear positivo
y = x – 5 → b = -5 → coeficiente linear negativo
y = -3x → b = 0 → coeficiente linear nulo
Coeficiente linear em uma função do 1° grau
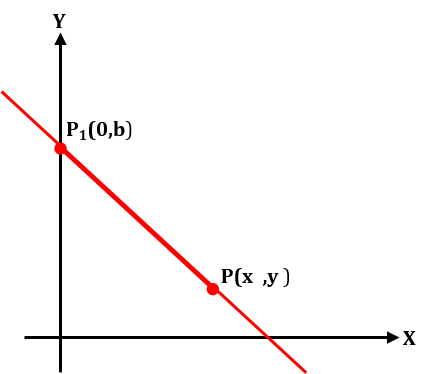
Uma reta y = ax + b expressa uma função do 1° grau da forma f(x) = ax + b. Na função do 1° grau, o coeficiente linear b, corresponde ao valor que a função assume quando x = 0, isto é:
f(0) = b
Quando a função é representada no plano cartesiano, o ponto de intersecção da reta com o eixo y é exatamente no ponto de coordenadas (0, b).
Exemplo: Na função f(x) = 2x – 3, o coeficiente linear é b = -3.
Veja que a reta corta o eixo y exatamente no ponto (0, -3).
Dessa forma, o coeficiente linear é um ponto importante na construção do gráfico de uma função do 1° grau, por isso, o ponto (0, b) é um dos pontos notáveis da função.
Você também pode se interessar: