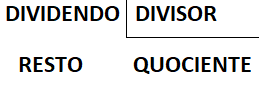Divisão – Aprender a fazer divisão com virgula
Entenda quando colocar a vírgula na divisão e como resolver divisão de números que já possuem uma vírgula, os números decimais.
A divisão é uma das operações matemáticas que costuma gerar mais dúvidas, principalmente quando envolve números decimais.
Os números decimais são aqueles números que aparecem escritos com uma vírgula.
A vírgula tem o papel de separar a parte inteira do número da parte não inteira. Por exemplo, no número 2,43, temos duas unidades inteiras e quarenta e três centésimos.
Em algumas situações, esses números aparecem no resultado da divisão de números que não tem vírgula. Mas em outras, os próprios números que queremos dividir já são números decimais. Cada caso é resolvido de uma forma diferente!
Antes de entender como resolver cada caso, veja quais são os elementos de uma divisão:
Divisão com vírgula no quociente
Nas divisões em que o dividendo for menor que o divisor, o quociente (resultado) será um número não inteiro, ou seja, um número com vírgula.
Para entender como fazer esse tipo de divisão, considere como exemplo dividir 3 por 5.
3 : 5 = ?
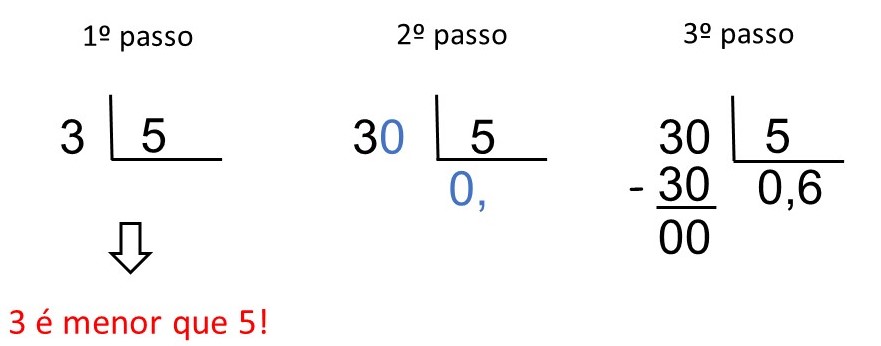
1º passo) Montamos a operação com a chave e verificamos que o o dividendo (3) é menor que o divisor (5), então, nessa operação vai aparecer uma vírgula no quociente.
2º passo) Como 3 é menor que 5, acrescentamos um zero (0) no dividendo que passa a ser 30 e acrescentamos um zero e uma vírgula (0,) no quociente.
3º passo) Dividimos 30 por 5 e escrevemos o resultado (6) no quociente.
Agora, vamos ver um outro exemplo, em que, inicialmente, o dividendo não é menor que o divisor. Contudo, em algum momento da operação vamos precisar dividir um número menor por um número maior.
Nesses casos, a vírgula também irá aparecer no quociente. Veja um exemplo: 63 : 5 = ?
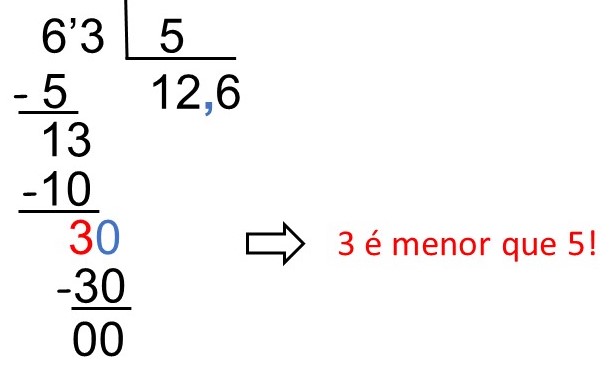
Quando montamos a divisão pelo método da chave, podemos observar que 63 é maior que 5. No entanto, quando resolvemos, obtemos quociente igual a 12 e resto igual a 3.
Então, nos deparamos com a divisão do exemplo anterior, 3 : 5.
O procedimento é semelhante, acrescentamos um zero ao lado do 3, que passa a ser 30, e acrescentamos uma vírgula no quociente.
Por que acrescentamos apenas uma vírgula e não um zero e uma vírgula, como fizemos antes? Porque, nesse caso, já temos um valor no quociente (12), que é a parte inteira do resultado da divisão.
Divisão com vírgula no dividendo e divisor
Muitas vezes queremos dividir um número decimal por um número inteiro ou o contrário, ou ainda, fazer uma divisão em que ambos os números sejam números decimais.
Exemplos:
3,8 : 2 17 : 0,5 9 : 6,4 0,2 : 0,8 10,9 : 4,5
Existem algumas formas de resolver esse tipo de conta. Um forma simples, consiste em “eliminar” a vírgula.
Para isso, devemos multiplicar ambos os números da divisão, dividendo e divisor, por um número estratégico, que nos permita resolver uma divisão equivalente à divisão inicial, mas sem vírgulas.
Sempre que multiplicamos um número decimal por 10, 100, 1000, …, a vírgula é deslocada para a direita conforme o número de zeros.
3,159 × 10 = 31,59 3,159 × 100 = 315,9 3,159 × 1000 = 3159
A ideia é multiplicar pelo número que “elimina” a vírgula. No caso de 3,159 seria multiplicar 1000.
Exemplo 1) calcular 2,8 : 7.
Para eliminar a vírgula do número 2,8, basta multiplicar por 10. Então, multiplicamos ambos os números da divisão por 10:
2,8 (x 10) : 7 (x 10) ⇔ 28 : 70
E resolvemos:
28 : 70 = 0,4
Portanto, 2,8 : 7 = 0,4.
Exemplo 2) calcular 10 : 0,25
Para eliminar a vírgula do número 0,25, basta multiplicar por 100. Então, multiplicamos ambos os números da divisão por 100:
10 (x 100) : 0,25 (x 100) ⇔ 1000 : 25
E resolvemos:
1000 : 25 = 40
Portanto, 10 : 0,25 = 40.
Exemplo 3) calcular 2,75 : 0,5
Para eliminar a vírgula do número 2,75, devemos por 100 e para eliminar a vírgula do número 0,5, multiplicar por 10.
Então, multiplicamos ambos os números da divisão por 100, pois os dois devem ser multiplicados pelo mesmo número:
2,75 (x 100) : 0,5 (x 100) ⇔ 275 : 50
E resolvemos:
275 : 50 = 5,5
Portanto, 2,75 : 0,5 = 5,5.
Você também pode se interessar: