Divisão de frações

Entenda o que é a divisão de frações e como realizar esse tipo de operação, a partir de exemplos simples e fáceis.

Você sabe o que significa a divisão de frações? Primeiramente, vamos nos lembrar que as frações são números como qualquer outro, então a divisão entre duas frações tem o mesmo sentido da divisão entre números naturais.

Por exemplo, dizemos que 8: 4 = 2, pois 4 × 2 = 8. E esse resultado significa que o número 4 cabe 2 vezes dentro do número 8, certo?

Com as frações, ocorre a mesma coisa. Se queremos dividir $\frac{1}{2}$ por $\frac{1}{6}$ , o que estamos querendo saber é quantas vezes o número $\frac{1}{6}$ cabe dentro do número $\frac{1}{2}$ .

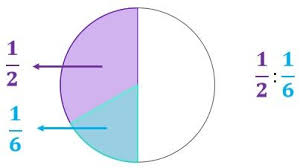
Para ficar mais claro, essa situação está representada na figura abaixo. Observe que a parte azul cabe 3 vezes dentro da parte roxa, ou seja, o número $\frac{1}{6}$ cabe 3 vezes dentro do número $\frac{1}{2}$ .

Logo, $\dpi{120} \mathbf{\frac{1}{2} : \frac{1}{6} = 3}$

Agora que já entendemos o que é a divisão entre frações, vamos ver uma forma prática de realizar essa operação sem precisar da ajuda de uma figura representativa.

Como fazer divisão de frações

Para fazer a divisão entre duas frações, basta conservar a primeira fração e multiplicar pelo inverso da segunda fração.

Lembre -se que:

O inverso de uma fração é obtido quando trocando o numerador de lugar com o denominador. Exemplo: o inverso de $\frac{{\color{Blue} 2}}{{\color{Red} 3}}$ é $\frac{{\color{Red} 3}}{{\color{Blue} 2}}$ .
Todo número inteiro pode ser escrito como uma fração de denominador 1. Exemplo: $5 = \frac{5}{1}$ . Assim, o inverso de 5 é $\dpi{120} \frac{1}{5}$ .

Além disso, devemos nos lembrar que para fazer a multiplicação entre frações, basta multiplicar o numerador da primeira fração pelo numerador da segunda fração e o denominador da primeira fração pelo denominador da segunda fração.

Então, vamos ver alguns exemplos de como fazer a divisão de frações.

Exemplos:

a) $\dpi{120} \frac{3}{10} : \frac{2}{9}$