Teorema de Pitágoras
O teorema de Pitágoras é muito utilizado na matemática e em outras áreas. Conheça sua fórmula e saiba como aplicar em problemas com triângulos.
O teorema de Pitágoras é um dos mais famosos da matemática, pois relaciona as medidas dos lados de qualquer triângulo retângulo e permite determinar suas medidas desconhecidas.
Os triângulos são figuras muito comuns no dia a dia, então, não só na matemática, mas também em outras áreas como arquitetura e engenharia, o teorema de Pitágoras tem diversas aplicações.
O teorema de Pitágoras é chamado assim em menção a Pitágoras, um grande físico e matemático nascido na Grécia há mais de 400 anos antes de Cristo.
O que é um triângulo retângulo?
Para compreender bem o teorema de Pitágoras, devemos entender o que é um triângulo retângulo, pois o teorema é aplicado a esse tipo de triângulo.
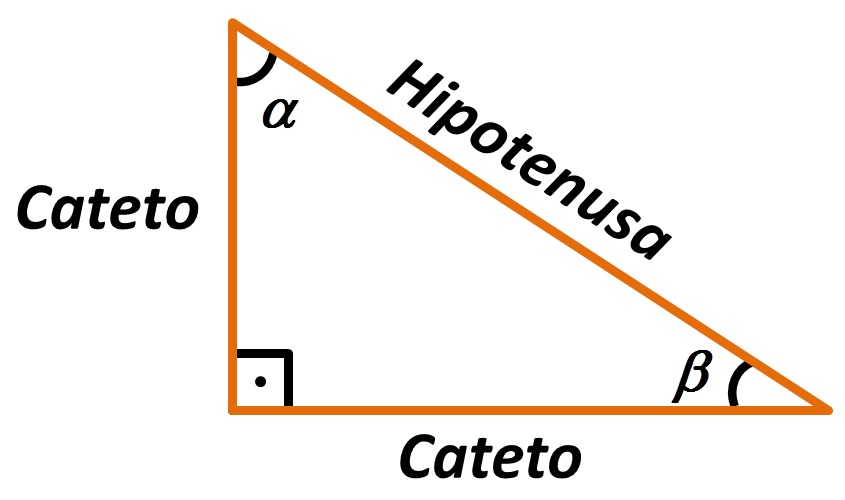
No triângulo retângulo, os lados recebem nome específicos, de acordo com a posição que eles estão em relação ao ângulo reto.
O lado oposto ao ângulo reto é chamado de hipotenusa e os lados que formam o ângulo reto, são chamados de catetos.
Uma observação importante sobre a hipotenusa, é que ela sempre corresponde ao maior lado do triângulo retângulo.
Qual a fórmula do teorema de Pitágoras?
O teorema de Pitágoras estabelece a relação que existe entre a hipotenusa e os catetos no triângulo retângulo.
De acordo com o teorema de Pitágoras: “a hipotenusa ao quadrado é igual a soma dos quadrados dos catetos”.
A fórmula do teorema de Pitágoras é:
Em que a é a medida da hipotenusa e b e c são as medidas dos catetos.
Exemplo:
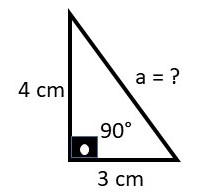
Determine a hipotenusa de um triângulo retângulo cujos catetos medem 4 cm e 3 cm.
Aplicando na fórmula, temos que:
a² = 3² + 4²
Elevando ao quadrado:
a² = 9 + 16
a² = 25
Extraindo a raiz quadrada em ambos os lados:
√a² = √25
a = 5
Portanto, a hipotenusa é igual a 5 cm.
Você também pode se interessar: