Área do trapézio

Aprenda a calcular a área do trapézio, conheça a fórmula e veja exemplos de como utilizá-la.

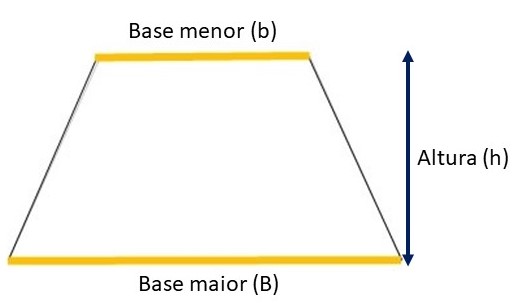
A área do trapézio corresponde à medida da sua superfície.

Relembre o que é um trapézio e suas principais características.

O trapézio é um polígono de quatro lados e por isso é chamado de quadrilátero. Ele possui dois lados opostos paralelos e os outros dois não paralelos.

Os lados paralelos são chamados de bases do trapézio, o de maior comprimento é a base maior e o de menor comprimento é a base menor.

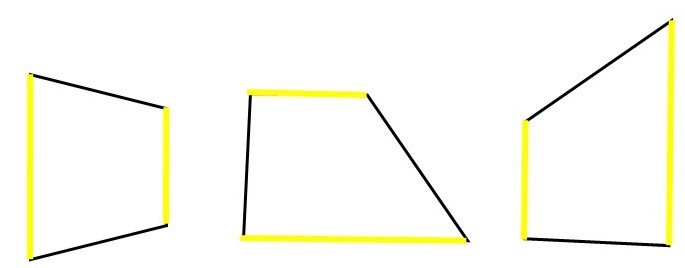
Há diferentes tipos de trapézios:

Veja a seguir como calcular a área do trapézio.

Fórmula da área do trapézio

A fórmula da área do trapézio é:

$\mathbf{A = \frac{(B + b)\cdot h}{2}}$

Em que:

A: área do trapézio;
B: medida da base maior do trapézio;
b: medida da base menor do trapézio;
h: altura do trapézio.

Observação: quando calculamos área, sempre obtemos uma medida elevada ao quadrado (m², cm², etc).

Exemplo 1:

Calcule a área de um trapézio com 8 centímetros de altura, 6 centímetros de base maior e 3 centímetros de base menor.

Temos h = 8 cm, B = 6 cm e b = 3 cm. Vamos aplicar esses valores na fórmula da área do trapézio:

$\mathrm{A = \frac{(6 + 3)\cdot 8}{2}}$

$\Rightarrow \mathrm{A = \frac{9\cdot 8}{2}}$

$\Rightarrow \mathrm{A = \frac{72}{2}}$

$\Rightarrow \mathrm{A = 36}$

Portanto, a área do trapézio é igual a 36 cm².

Exemplo 2:

Calcule a altura de um trapézio de área igual a 40 cm² , 10 centímetros de base maior e 6 centímetros de base menor.

Temos A = 40 cm², B = 10 cm e b = 6 cm. Vamos aplicar esses valores na fórmula da área do trapézio para determinar a altura.

$\mathrm{40 = \frac{(10 + 6)\cdot h}{2}}$

$\Rightarrow \mathrm{80 = (10 + 6)\cdot h}$

$\Rightarrow \mathrm{80 = 16\cdot h}$

$\Rightarrow \mathrm{h = \frac{80}{16}}$

$\Rightarrow \mathrm{h = 5}$

Portanto, a altura do trapézio é igual a 5 cm.

Você também pode se interessar:

Continue lendo

Geometria plana