Área do triângulo
A área de uma figura plana corresponde à medida da sua superfície. Aprenda a calcular a área do triângulo, veja a fórmula e exemplos!
A área do triângulo corresponde à medida da sua superfície.
Vamos relembrar o que é um triângulo e suas características para entender como calcular sua área.
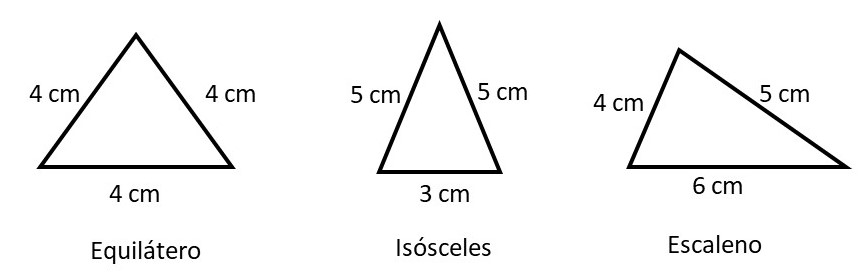
O triângulo é um polígono que possui três lados e três ângulos internos. Em relação às medidas dos lados, os triângulos são classificados em: equilátero, isósceles ou escaleno.
- Triângulo equilátero: possui todos os lados com tamanhos iguais;
- Triângulo isósceles: possui dois lados com tamanhos iguais;
- Triângulo escaleno: possui todos os três lados com tamanhos diferentes.
Veja a seguir como calcular a área do triângulo.
Fórmula da área do triângulo
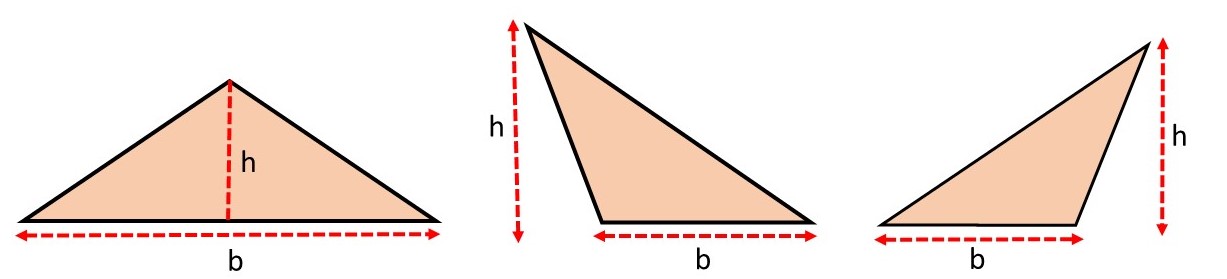
Para calcular a área do triângulo, é necessário conhecer a sua altura e a medida da sua base. A base do triângulo pode ser qualquer um dos seus três lados, mas de acordo com a base a altura irá variar.
Nas figuras a seguir, temos um mesmo triângulo em posições diferentes. Para cada base (b), temos uma altura (h) correspondente. Um mesmo triângulo pode ter até três medidas diferentes de altura.
Considerando a base e sua altura correspondente, a fórmula da área do triângulo é:
Em que:
- A: área do triângulo;
- b: medida da base do triângulo;
- h: altura do triângulo.
Observações:
- O resultado obtido na fórmula da área deve ser sempre o mesmo para qualquer uma das bases e altura que estivermos considerando de um triângulo.
- Quando calculamos área, sempre obtemos uma medida elevada ao quadrado (m², cm², etc).
Exemplo 1:
Calcule a área de um triângulo de base 10 cm e altura correspondente a 6 cm.
Temos b = 10 cm e h = 6 cm. Vamos aplicar esses valores na fórmula da área do triângulo:
Portanto, a área do triângulo é igual a 30 cm².
Exemplo 2:
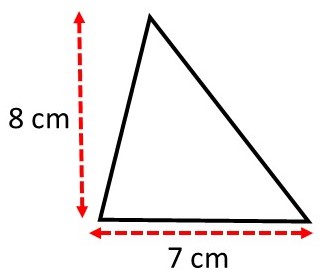
Calcule a área de um triângulo com as dimensões apresentadas na figura abaixo:
Temos b = 7 cm e h = 8 cm. Vamos aplicar esses valores na fórmula da área do triângulo:
Portanto, a área do triângulo é igual a 28 cm².
Você também pode se interessar: