Coeficiente angular

Saiba o que é o coeficiente angular da reta. Veja as formas de calcular!

O coeficiente angular é um valor associado ao estudo da equação da reta, indicando o quanto a reta está inclinada em relação ao eixo das abscissas (eixo x) em um sistema de coordenadas.

Na equação reduzida da reta, o coeficiente angular é o valor que aparece multiplicando a variável independente x.

Equação reduzida da reta:

$\dpi{120} \mathrm{y = \mathbf{m}x + \mathbf{b}}$

m: coeficiente angular.
b: coeficiente linear.

Exemplo:

Encontre o coeficiente angular em cada uma das retas:

a) $\mathrm{y = 3x + 1}$ ⇒ m = 3

b) $\mathrm{y = -x + 12}$ ⇒ m = -1

c) $\mathrm{y = 0,5x}$ ⇒ m = 0,5

Quando a equação da reta estiver em sua forma geral, devemos escrevê-la em sua forma reduzida, para obter o coeficiente angular:

Exemplo:

Determine o coeficiente angular da reta $\mathrm{2y - 8x + 6 = 0}$ .

Isolando y, escrevendo na forma reduzida:

$\mathrm{y= \frac{8x}{2} - \frac{6}{3} }$

$\mathrm{y= 4x - 2 }$

Portanto, o coeficiente angular é m = 4.

Como calcular o coeficiente angular

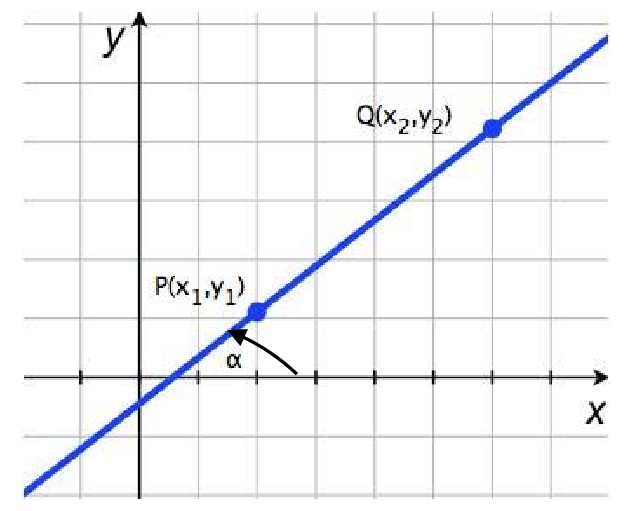
O coeficiente angular pode ser calculado a partir do ângulo de inclinação da reta ( $\dpi{120} \alpha$ ) ou a partir de dois pontos quaisquer pertencentes a reta $\dpi{120} \mathrm{P(x_1, y_1)}$ e $\dpi{120} \mathrm{Q(x_2, y_2)}$ .